问：

我们正在我们的数据中心实现 Erlang C 计算，我遇到了一个障碍：
SQL Server 数据类型的溢出错误。float

如何在 SQL Server 中表示超过 10^308 的值，以便我仍然可以执行算术运算？

Erlang C 计算回答了这个问题，“给定预测的呼叫量和估计的处理时间，我们应该安排多少座席来确保在指定时间内有足够比例的呼叫者得到答复？

举个例子：我们的服务水平是 75% 的电话必须在 60 秒内接听。下表探讨了与我们运营相关的各种数量和处理时间的人员配备。

您可以看到，当所需的代理数超过 140 时，SQL Server 无法再处理所需数量的大小。

这里的问题是公式中间的幂和阶乘项。
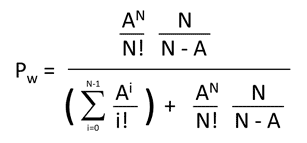]2
例如，导致第一个错误的计算具有 V=425 和 AHT=600：
（425 次调用/30 米 @ 10 米/次调用 -> 141 次调用小时/小时 -> 141 个 erlangs） A=141 从 n=142
开始评估

当 N=142 时，A^N 是 3.02002e+305 和 N！是 2.69536e+245。完成计算会产生大约 6% 的服务级别，这是不够的。
当 N=143 时，A^N 是 4.27836e+307 和 N！是 3.85437e+247。完成计算后，服务级别约为 24%，但这仍然不够。
对于 N=144，A^N 为 6.06101e+309，当我尝试计算它时，SQL Server 会生成一个错误，因为该类型最多只能处理大约 1e308 的数字。float

编辑：

@chtz和@dmuir给了我需要的提示。
而不是积累 A^i 和 i！另外，我按照建议将它们累积在一起，新版本完美运行。

SELECT 
    @acc_ai_if = @acc_ai_if * @intensity / cast(@agentcount as float)
--  @acc_if = @acc_if * @agentcount
--, @acc_ai = @acc_ai * @intensity  -- this overflows for N>143
;

sql-server 浮点精度 biginteger 电话呼叫

#include    <stdio.h>
#include    <stdlib.h>

    // compute beta(toN) from A and previous value of beta
    static  double  beta_step( int A, int toN, double beta)
    {
    double  f = A/(double)toN;
        return f*beta/(1.0+beta);
    }
    int main( void)
    {
    int A = 140;
    int np = 20;    // number of probabilities to compute
        // compute values for beta at N=1..A    
    double  beta = A;
        for( int N=2; N<=A; ++N)
        {   beta = beta_step( A, N, beta);
        }
        // compute probabilities at N=A+1..A+np
        for( int i=1; i<=np; ++i)
        {
        int N = A+i;
            beta = beta_step( A, N, beta);
        double  f = (double)N/(double)i;    // == N/(N-A)
        double  prob = f*beta/(f*beta + 1.0);   
            printf( "%d\t%f\n", N, prob);
        }   
        return EXIT_SUCCESS; 
    }

我编译了这个（使用一个相当古老的 gcc （4.8.5））

gcc -o erl -std=gnu99 -Wall erl.c

0赞 Rosenfeld Eugen 3/16/2021 #2

在 SQL Server 中计算 A=341 和 N=1000 的 ErlangC

DECLARE @startnum float=1
DECLARE @X float = 1

DECLARE @A float= 341
DECLARE @N float= 1000
;
WITH comp AS (
    SELECT @startnum as num,@A as res
    UNION ALL
    SELECT num+1, res*@A/(num+1) FROM comp WHERE num<@N 
)
SELECT res*(@N/(@N-@A))/((SELECT SUM(res) FROM comp where num<@N)+res*(@N/(@N-@A))) FROM comp where num=@N
option (maxrecursion 32000)

上一个：从 varchar 转换为十进制而不会损失精度

下一个：对 SQL Server 浮点数和 SQLCMD 返回的误解

当浮点数据类型太小时，如何在 SQL Server 中计算 Erlang C 值？

How can I calculate Erlang C values in SQL Server when the float datatype is too small?

编辑：

评论